Determining the optimal fractional charge σ

For high-TC superconductors, the optimal transition temperature TC0 is given by the algebraic expression:

TC0 = β [ση/A)]1/2 ζ−1 ,

where σ is the fractional charge per formula unit in a layer of the type I reservoir (an outer layer in cases of ν = 2), corresponding to surface area A. The interaction occurs between two charge reservoirs (type I and type II) of opposite sign, separated by the nearest-neighbor interaction distance ζ , where η is the number of charge-carrying layers in the type II reservoir, ℓ−2 ≡ [ση/A] is the areal charge density per type I layer per formula unit for participating carriers, and β [= kB-1 (0.1075 ± 0.0003 eV-Å2) ≡ e2Λ / kB-1] is a universal constant. Note that the length Λ is approximately twice the reduced electron Compton wavelength. There are two methods of determining σ as described below.

Charge Allocation Methodology(LaBa)2CuO4-d

Whereas A and ζ are readily determined from crystal structure and η is determined by inspection, the fractional charge σ is much more elusive. In general, doping may be either cation or anion, and can occur in the type I reservoir, as in the case of La2−xSrxCuO4, the type II reservoir, e.g. Ba2Y(Ru1−xCux)O6 or in both; the binary and ternary iron chalcogenide systems (e.g. KxFe2−ySe2 [2]) have as many as two dopant ions, one from each reservoir. Thus, for the compounds discussed herein, σ can be determined by considering the cation and anion doping according to,

σ = γ[|vI(x – x0)I| + |vII(x – x0)II|]  ,

where vi is the net charge due to dopants (typically the valence difference between the dopant and the native ion) in reservoir i, (x − x0)i is the generic doping factor in which x denotes the content of the dopant species (e.g. x in AxB) and x0 is the minimum value of x required for superconductivity. The above equation is a generalization of equation (2.4a) from Ref. [1], which incorporates the possibility of non-unit valence doping and contains two terms corresponding to the two charge reservoirs; the absolute values confine the summation to the magnitudes of the individual contributions to σ. The factor γ derives from the allocation of the dopant charge by considering a given compound’s structure. To calculate σ for a given compound, the modifying factor γ is determined by application of the set of rules developed in [1]; the following (first set of) charge allocation rules are apply:

(1a) Sharing between N (typically 2) ions or structural layers introduces a factor of 1/N in γ.

(1b) The doping is shared equally between hole and electron reservoirs resulting in a factor of 1/2.

Multiple charge sources in opposing reservoirs (e.g. determined by K and Fe stoichiometries in KzFe2−ySe2) are treated as a single contribution to σ (hence the absolute values), with γ determined by rules (1a) and (1b). Numerous high-TC materials share the same value of σ as optimal YBa2Cu3O6.92, which we have denoted σ0 and determined to have the value 0.228. For those compounds where the (x − x0)i cannot be discerned independently through doping, σ can be calculated by scaling to σ0 according to σ = γ σ0 , where γ is defined in conjunction with a second set of (stoichiometric) scaling rules that are discussed below.

An example of the application of charge allocation is provided by La1.837Sr0.163CuO4–δ (TC0meas = 38 K).  Since x0 = 0, the total charge doping is 0.163. This charge is accordingly distribution between the type I and type II reservoirs, thereby introducing a factor of 1/2 in γ [rule (1b)]. As there are two SrO layers in the type I reservoir (i.e., ν = 2) rule (1a) provides an additional factor of 1/2 [1]:

  • σ = (0.163)(1/2)(1/2) = 0.048
  • η = 1; ν = 2
  • A = 14.2268 Å2; ζ = 1.7828 Å
  • TC0calc = 37.47 K

Stoichiometric Scaling Methodology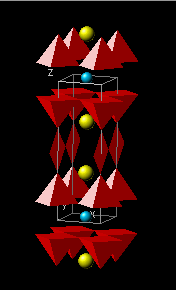REBa2Cu3O7-d

Also termed “Valency Scaling,” this approach assumes that the optimal fractional charge σ for all cuprate superconductors are proportional to that of YBa2Cu3O6.92 (denoted as σ0), where the scaling factor γ is dependent upon electronic and structural parameters of a given cuprate in relation to YBa2Cu3O6.92. Thus one can write [1]:

σ = γσ0  ,

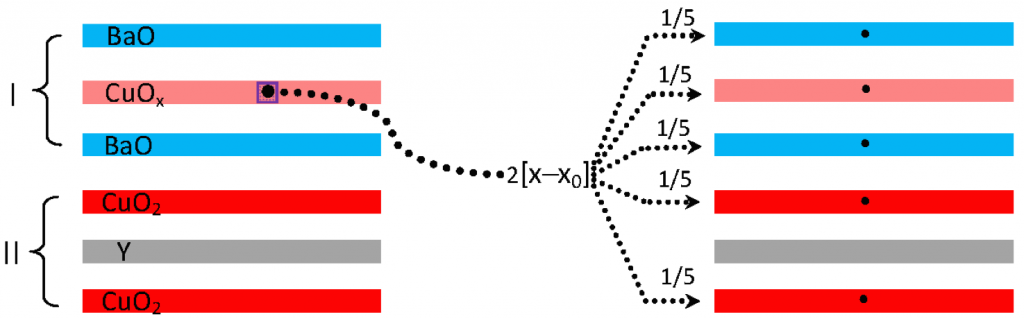
where σ0 is considered a fundamental quantity. To determine σ0, one considers oxygen content x above the minimum value (x0 = 6.35 [1]) required for superconductivity to occur. The total oxygen content associated with the optimal superconductive state is then, (6.92 – 6.35) = 0.57.  Given a valence of –2 per oxygen ion, the total number of carriers available to dope the superconducting structure is 2×0.57 = 1.14. As there are five oxygen-containing layers, two CuO2 layers, two BaO layers and one CuO layer, and assuming that all five layers are populated equally, σ0 = 1.14/5 = 0.228.

Since η = 2, A = 14.8596 Å and ζ = 2.2677 Å [1], TC0calc is found to be 96.36 K, which agrees well with the measured value of TC0meas = 93.78 K. There are three rules governing the value of γ [1,3]:

(2a) Heterovalent substitution in the type I inner layer(s) of a +3 (or +1) ion mapped to a +2 ion, corresponding to the YBa2Cu3O6.92 structural type, introduces a factor of 1/2 (or 2) in γ.

(2b) The factor γ scales with the +2 (–2) cation (anion) structural and charge stoichiometry of the participating charge.

(2c) The factor γ scales with the net valence of the undoped mediating layer.  

Rules (2a) and (2b) are specific to optimal cuprates superconductors. Moreover, the electronegativity χ of the substituted cation, relative to that of Cu (χ = 1.90), can affect charge-transfer efficacy: High electronegativity cations, such as Pb (χ = 2.33) and Bi (χ = 2.02), suppress charge transfer, resulting in an additional factor of 1/2 in γ. Cations with comparatively low electronegativities, such as Tl (χ = 1.62), do not impede charge transfer, and thus do not induce an additional γ-factor [3]. This understanding provides an explanation for the dichotomy in optimal transition temperatures between Tl-and Bi-based homologues. Rule (2c) allows scaling between YBa2Cu3O6.92 and other superconducting families, given a one-to-one structural correspondence [1].

An example of the application of stoichiometric scaling is provided by YBa2Cu3O6.60. Using rule (2b), σ for the “60 K” phase material can be similarly obtained as with the “90 K” material, but with a participating charge of 2 (6.60 – 6.35)/5 = 0.1. However, one obtains the same answer by simply scaling the oxygen (anion) content above x0 = 6.35 relative to that of YBa2Cu3O6.92. Therefore, one has [1]:

  • σ = [(6.60 – 6.35)/(6.92 – 6.35)] σ0 = 0.439 σ0 = 0.1
  • η = 2
  • A = 14.8990 Å2; ζ = 2.2324 Å
  • TC0meas = 63 K; TC0calc = 64.77 K
  1. D. R. Harshman, A. T. Fiory and J. D. Dow, J. Phys.: Condens. Matter 23, 295701 (2011); 23, 349501 (2011).
  2. D. R. Harshman and A. T. Fiory, J. Phys.: Condens. Matter 24, 135701 (2012).
  3. D. R. Harshman and A. T. Fiory, J. Phys. and Chem. Solids 85, 106 (2015).

Comments are closed.