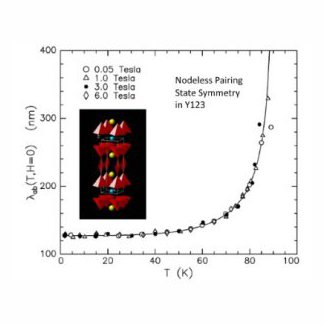
The ground-state symmetry of the high-TC dominant superconductive state is well established to be nodeless, consistent with strongly-coupled s-wave, or extended s-wave pairing. This was first demonstrated for sintered cuprate YBa2Cu3O7−δ in 1987 [Physical Review B 36, 2386 (1987)], and later for single-crystal YBa2Cu3O7−δ [Physical Review B 39, 851 (1989)] using muon spin rotation (μ+SR). The μ+SR technique is particularly well suited for such a determination since it directly probes the bulk mixed state. Very interesting fluxon motion and pinning behaviors are also observable which, when properly understood and modeled, allows the extraction of the true temperature-dependent magnetic penetration depth, λ(T), as is illustrated in an exhaustive study of λ(T,H) in a high-quality single crystal of YBa2Cu3O7−δ [Physical Review B 69, 174505 (2004)] [post]. These results (i) confirm the s-wave superconductivity character originally observed in 1987, and (ii) show that the features of μ+SR (and microwave) data claimed by other authors to be evidence for d-wave superconductivity are instead symptomatic of temperature-dependent depinning of vortices, which results in long-ranged distortion of the flux lattice. Indeed, the probability that any published d-wave model gives a better fit than the two-fluid model is less than 4×10-6.
Muon spin rotation (μ+SR) measurements of square root second moment σ of local magnetic fields in superconducting mixed states, as published for oriented crystals and powder samples of YBa2Cu3O7–δ (δ ≈ 0.05), YBa2Cu4O8 and La2-xSrxCuO4 (x ~ 0.15–0.17), are further subjected to comparative analysis for superconducting gap symmetry in [Journal of Physics: Condensed Matter 23, 315702 (2011] [post]. For oriented crystals it is shown that anomalous dependences of σ on temperature and applied field H, as-measured and extracted a– and b-axial components, are attributable to fluxon depinning and disorder that obscure the intrinsic character of the underlying superconducting penetration depth. Random averages derived from oriented crystal data differ markedly from corresponding non-oriented powders, owing to the weaker influence of pinning in high-quality crystals. Related indicators for pinning perturbations such as non-monotonic H dependence of σ, irreproducible data and strong H dependence of apparent transition temperatures, are also evident. Strong intrinsic pinning suppresses thermal anomalies in c-axis components of σ, which reflect nodeless gap symmetries in YBa2Cu3O7–δ and YBa2Cu4O8. For YBa2Cu3O7–δ, the crystal (a–b components, corrected for depinning) and powder data all reflect a nodeless gap (however, a–b symmetries remain unresolved for crystalline YBa2Cu4O8 and La1.83Sr0.17CuO4. Inconsistencies contained in multiple and noded gap interpretations of crystal data, and observed differences between bulk μ+ and surface-sensitive measurements are discussed therein.
The muon-spin-relaxation (μSR) technique has been used to study the internal field modulation dynamics of fluxons in crystals of κ-[BEDT-TTF]2Cu[NCS]2 (TC ≊ 10.5 K) Physical Review B 49, 12990 (1994). The data exhibit a strong field dependence for applied fields in the range 129 Oe ≤ ‖Hext‖ ≤ 4 kOe, which is attributed to a combination of vortex motion, finite core size effects, and pinning. In low fields (‖Hext‖ = 129 Oe), the data exhibit a flux-pinning transition at TX ∼ 5 K, as evidenced by a peak in the second moment of the local field distribution at ∼5 K accompanied by an enhanced minimum in the first moment at the same temperature. In higher fields (‖Hext‖ = 750 Oe, 3 kOe, and 4 kOe), where the effects of motion and pinning are minimized, the symmetry of the underlying gap function is confirmed as s wave. Corrections for finite fluxon core, finite mean free path, and flux-lattice disorder were applied in determining the London penetration depth, λL(𝑏𝑐)(0) = 7680±700 Å.