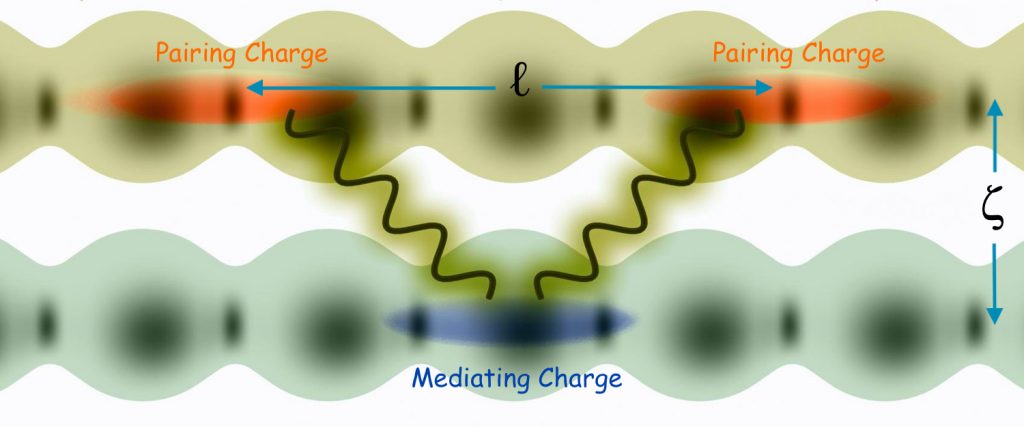
Pairing in high-TC superconductors is mediated by Compton scattering of virtual photons between two charge reservoirs; type I and type II [1]. Typically, the type I reservoir hosts the primary superconducting condensate while the type II reservoir provides mediating charges. However, in the case of H3S, for example, the two reservoirs are identical and perform both roles. As presented elsewhere, the optimal transition temperature for high-TC superconductors obey the algebraic equation,
TC0 = β (ση/A)–1/2 ζ–1 = kB–1 (Λ/ℓ) e2/ζ ,
where β (= 1247.4 K-Å2) and Λ (= 0.007465 Å) are universal constants, the latter approximating twice the reduced Compton wavelength, ℓ-1 = [ση/A]–1/2 is the interaction charge density, σ is the charge fraction of one of the type I layers, η is the number of charge-carrying type II layers, and A is the area per formula unit of the type I reservoir layer or surface. Part of the above equation, the Coulomb potential e2/ζ factor, was previously derived (see section 3 of [2]) by drawing an analogy with Allen-Dynes theory [3], which considers BCS superconductivity in the strong-coupling limit, obtaining TC ∝ (〈ω2〉λ)1/2, where ω2〉is the average square phonon frequency and λ the electron-phonon coupling parameter, with Coulomb repulsion being ignored [4]. This derivation evaluates〈ω2〉λ by an integral over the Fermi surface of the square of electron-ion interaction forces. Evaluated in real space and determined by the inter-reservoir electronic Coulomb interaction (assumed to be unscreened within the unit cell [5]), the force is given as F(r) = ±e2r (r2 + ζ2)–3/2, which is constrained to the in-plane or longitudinal component for electronic charges in surfaces separated by a transverse distance ζ and projected in-plane radial distance r. Integrating 2πrF2(r) over r from 0 to ∞ and taking the square-root yields (π/2)1/2e2/ζ, whence the factor e2/ζ in TC0 is obtained. In practice, this interaction is local, corresponding to a limited range of integration, r ≤ ζ; this results in the same potential factor, but with a smaller numerical coefficient.
The origin of the factor Λ/ℓ in equation (1) may be understood by considering the Compton scattering probability. Owing to thermal smearing of both the Fermi surface and superconducting gap, one expects ample phase space for quasiparticle creation by Compton scattering events. The essentially instantaneous nature of quasiparticle creation, compared to the significantly slower relaxation process, allows for unscreened Coulomb interactions between electronic charges in adjacent reservoirs. Equation (1) thus derives fundamentally from quantum fluctuations within the virtual photon field between the two charge reservoirs inducing Compton scattering of quasiparticles confined essentially within their respective reservoirs.
Scattering of a quasiparticle from an initial equilibrium state k on the Fermi surface to a final state k’ via a Compton scattered virtual photon precipitates a corresponding shift from q to q’ in the photon wavevector. The final state wavevector k’ is expected to contain a small transverse component, such that k and k’ remain essentially transverse to the direction of the separation distance ζ. Such electron-photon scattering events can be likened to the problem of electron-impurity scattering, where transport electrons confined to near the Fermi surface with Fermi wavevector kF are scattered by real space localized potentials with a mean free path spacing of ℓmfp; the probability for a single such scattering event scales as (kFℓmfp)–1. In the Compton scattering picture, virtual photons of wave vector q confined within the real space region between the two interacting reservoirs defined by ζ act in analogy to transport electrons and scatter off of the essentially localized electrons/holes of spacing ℓ (acting in analogy to impurities). The analogy entails a tenable difference between electron and photon time scales, given Fermi velocity vF << c. Thus, the probability of scattering a virtual photon from initial state q to final state q’ is given by the differential (q’ℓ)–1 – (qℓ)–1 = Δƛℓ–1 = ƛC(1 – cos θ)ℓ–1, where ƛC = ћ/mec is the reduced Compton wavelength and θ is the angle between the incident and scattered photons (note that setting θ = π yields Δƛ = 2ƛC). The momentum perturbation associated with electron recoil is very small, since |q – q’| << kF for virtual photons of energy e2/ζ. Identifying Λ as proportional to ƛC and integrating over the relevant angles of the incident and scattered photons one obtains,
TC0 ∝ (ƛC/ℓ) e2/ζ ,
a result which can be (holistically) interpreted as the product of the scattering probability and the energy of the scattering interaction. Thus, the mediation of the high-TC superconducting state is facilitated through Compton scattering between virtual photons and unscreened quasiparticles.
- D. R. Harshman and A. T. Fiory, J. of Phys.: Condens. Matter 29, 445702 (2017).
- D. R. Harshman, A. T. Fiory and J. D. Dow, J. Phys.: Condens. Matter 23, 295701 (2011); 23, 349501 (2011).
- P. B. Allen and R. C. Dynes, Phys. Rev. B 12, 905 1975.
- See Eq. (25) in [2]
- C. M. Varma, S. Schmitt-Rink, and E. Abrahams, Solid State Commun. 62, 681 (1987)











