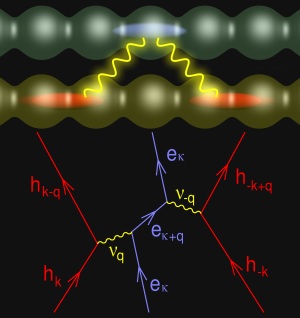
High-TC superconductivity

htc_interaction_image_sm

High TC superconductivity originates from the Coulomb interaction between two adjacent charge reservoirs; the type I reservoir hosts the superconducting condensate with areal charge fraction σI (per formula unit) while the type II reservoir contains the mediating charges fraction σII. Given ν (= 1, 2) type I interacting layers and η type II charge-carryiing component layers, the optimal superconducting state is achieved when the two reservoirs are in equilibrium defined by [1, 7, 10],

νσI = ησII .

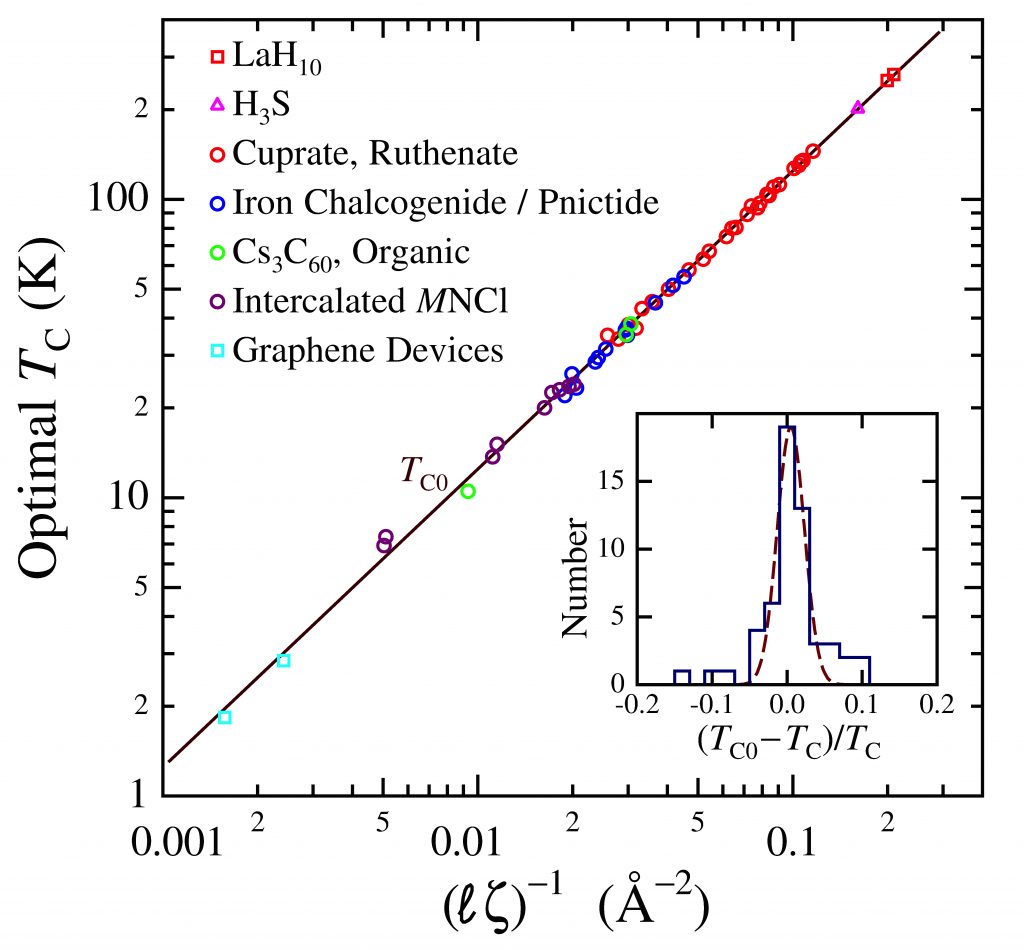
Remarkably, the optimal transition temperature TC0 is independent of band structure, Fermi energy, effective mass, etc., determined completely by the interacting charge number density and the separation between the two reservoirs according to the algebraic expression [1],

TC0 = kB−1 β (ση/A)1/2 ζ−1 = kB−1 (Λ/ℓ) e2/ζ

where ζ is the interaction distance (along the transverse axis), σ/A (=σI/AI) is the optimal areal charge density per type I layer per formula unit for participating charges, η is the number of mediating layers (e.g., the number of cuprate planes), and β (= 0.1075 ± 0.0003 eV Å2) is a universal constant; Λ = e–2β is approximately twice the reduced electron Compton wavelength. Rules for determining σ are discussed here (see also, Notes), and the relevant experimental parameters and the calculated values of TC0 are listed under Tabulated results for 58 optimal high-TC materials from eleven superconductor families [1-12].

Evidence of the Coulomb potential e2/ζ is found in optical reflectance data in the mid-infrared range for Cs3C60 [7], and H3S [8], where the electronic contribution (ωχ) is given as,

ℏωχ = e2/ε∞ζ,

where ε∞ is the high-frequency dielectric constant.

Note: the pairing interaction model, first introduced in 2011 [1] has since been further developed and expanded by Dale R. Harshman and Anthony T. Fiory [2-12]. The term, “high-TC” (meaning “high transition temptation superconductivity), is somewhat of a misnomer; while the mechanism allows for extremely high transition temperatures, it is applicable to low-TC materials as well.

  1. D. R. Harshman, A. T. Fiory and J. D. Dow, J. Phys.: Condens. Matter 23, 295701 (2011); 23 349501 (2011).
  2. D. R. Harshman and A. T. Fiory, J. Phys.: Condens. Matter 24, 135701 (2012).
  3. D. R. Harshman and A. T. Fiory, Phys. Rev. B 86, 144533 (2012).
  4. D. R. Harshman and A. T. Fiory, J. Phys. Chem. Solids 85, 106 (2015).
  5. D. R. Harshman and A. T. Fiory, Phys. Rev. B 90, 186501 (2014).
  6. D. R. Harshman and A. T. Fiory, J. Supercond. Nov. Magn. 28, 2967 (2015).
  7. D. R. Harshman and A. T. Fiory, J. Phys.: Condens. Matter 29, 145602 (2017).
  8. D. R. Harshman and A. T. Fiory, J. Phys.: Condens. Matter 29, 445702 (2017).
  9. D. R. Harshman and A. T. Fiory, J. Supercond. Nov. Magn. 33, 367 (2020).
  10. D. R. Harshman and A. T. Fiory, J. Supercond. Nov. Magn. 33, 2945 (2020).
  11. D. R. Harshman and A. T. Fiory, J. Appl. Phys. 131, 015105 (2022).
  12. D. R. Harshman and A. T. Fiory, {arXiv] [post]

Comments are closed.