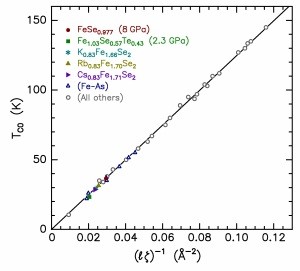
The Superconducting Transition Temperatures of Fe1+xSe1-y, Fe1+xSe1-yTey and (K/Rb/Cs)zFe2-xSe2), D. R. Harshman and A. T. Fiory [arXiv]
In a recent contribution to this journal, it was shown that the transition temperatures of optimal high-Tc compounds obey the algebraic relation, TC0 = kB–1β/ℓζ, where ℓ is related to the mean spacing between interacting charges in the layers, ζ is the distance between interacting electronic layers, β is a universal constant and kB is Boltzmann’s constant. The equation was derived assuming pairing based on interlayer Coulomb interactions between physically separated charges. This theory was initially validated for 31 compounds from five different high-TC families (within an accuracy of ±1.37 K). Herein we report the addition of Fe1+xSe1–y and Fe1+xSe1–yTey (both optimized under pressure) and AzFe2–xSe2 (for A = K, Rb, or Cs) to the growing list of Coulomb-mediated superconducting compounds in which TC0 is determined by the above equation. Doping in these materials is accomplished through the introduction of excess Fe and/or Se deficiency, or a combination of alkali metal and Fe vacancies. Consequently, a very small number of vacancies or interstitials can induce a superconducting state with a substantial transition temperature. The confirmation of the above equation for these Se-based Fe chalcogenides increases to six the number of superconducting families for which the transition temperature can be accurately predicted.
 Schematic diagram of (a) Fe1+xSe1–y and (b) KxFe2–ySe2, as projected views along their [110] directions (linear densities of tetrahedrally-coordinated Fe are twice those of Se), illustrating the structures of the type I and type II reservoirs, the periodicity d and the interaction distance ζ. Vacancies and excess atoms are not shown. |
 The optimal superconducting transition temperature TC0 plotted against (ℓζ)-1, where ℓ is the mean in-plane distance between participating charges and ζ is the distance between interacting layers. The five 11 and 122 Fe chalcogenides (solid symbols) are compared to the 1111 and 122 Fe pnictides (open triangles) and the remainder of the thirty-six compounds (open circles), exhibiting behaviors in agreement with theory, represented by solid line. |
D. R. Harshman and A. T. Fiory, J. Phys.: Condens. Matter 24, 135701 (2012).
