Modeling Intercalated Group-4-Metal Nitride Halide Superconductivity with Interlayer Coulomb Coupling

Modeling Intercalated Group-4-Metal Nitride Halide Superconductivity with Interlayer Coulomb Coupling, D. R. Harshman and A. T. Fiory [arXiv]

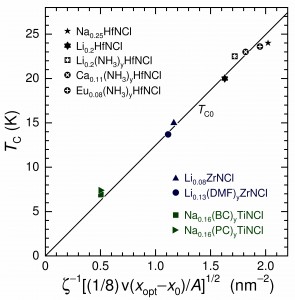
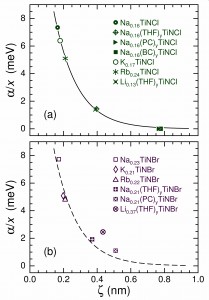
Behavior consistent with Coulomb-mediated high-T_C superconductivity is shown to be present in the intercalated group-4-metal nitride halides A_x(S)_yMNX, where the MNX host (M = Ti, Zr, Hf; X = Cl, Br) is partially intercalated with cations A_x and optionally molecular species (S)_y in the van der Waals gap between the halide X layers, expanding the basal-plane spacing d. The optimal transition temperature is modeled by T_C0 ∝ ζ^–1(σ/A)^1/2, where the participating fractional charge per area per formula unit σ/A and the distance ζ, given by the transverse A_x–X separation (ζ < d), govern the interlayer Coulomb coupling. From experiment results for β-form compounds based on Zr and Hf, in which concentrations x of A_x are varied, it is shown that σ = γ[v(x_opt − x₀)], where x_opt is the optimal doping, x₀ is the onset of superconducting behavior, v is the A_x charge state, and γ = 1/8 is a factor determined by the model. Observations of T_C < T_C0 in the comparatively more disordered α-A_x(S)_yTiNX compounds are modeled as pair-breaking by remote Coulomb scattering from the A_x cations, which attenuates exponentially with increasing ζ. The T_C0 values calculated for nine A_x(S)_yMNCl compounds, shown to be optimal, agree with the measured T_C to within experimental error. The model for T_C0 is also found to be consistent with the absence of high-T_C characteristics for A_xMNX compounds in which a spatially separated intercalation layer is not formed.

Plot of measured transition temperature TC versus ζ−1[(1/8) v(xopt − x0)/A]1/2 for the high-TC compounds listed in Table 1 and compounds with α = 0 from Table 2. Interaction distance ζ is from Eq. (1), v(xopt − x0) is the optimal doping xopt relative to the superconductivity onset value x0 and multiplied by valence v, and A is basal area per formula unit. The line represents TC0 for optimal compounds from Eq. (6).

Pair breaking parameter α from Table 2 normalized to alkali content x and plotted against interaction distance ζ for the α-form compounds, (a) Ax(S)yTiNCl and (b) Ax(S)yTiNBr. The curves represent the function of Eq. (5) fitted to the Ax(S)yTiNCl compounds.

Dale R. Harshman and Anthony T. Fiory, J. Supercond. Nov. Mater. 28, 2967 (2015).